Solution to: Men on the Moon
From the first part of this puzzle, we know that the radius of the circle with a circumference of the cable's length is 1/(2×pi) meters less than the moon's radius. In the figure shown below, therefore
x = r - 1/(2×pi)
and
cos(a) = x / r = (r - 1/(2×pi)) / r
and, when taking a in radians,
y = (a / (2×pi)) × (2×pi×r) = a × r.
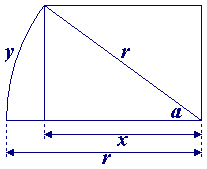
Since r=3476000/2=1738000 meters, we can calculate that y is approximately 744 meters, which is the distance that the cable should be laid north of the moon's equator to settle the problem of the lacking 1 meter of cable.