 |
| |
|
|
|
|
|
The puzzles are marked with stars ( ) that show the degree of difficulty of the given puzzle. | |
|  back to the main puzzle page.
| |
|
Copyright © 1996-2010. RJE-productions. All rights reserved. No part of this website may be published, in any form or by any means, without the prior permission of the authors.
| |
|
Eight Queens 
| | 
| |
|
This is a commonly known chess problem...
| |
 |
The Question:
In how many ways can you arrange
8 queens on a standard chess-board in such a way that none of them is
attacking any other?
| |
 |
The Answer:
Click here!...
| |
|
 back to index
| |
|
Names & Numbers
| | 
| |
|
Thanks to Mike and Ruth VanderMeer from Canada, we
can present you the following names and numbers puzzle:
Four words add up to a fifth word numerically:
mars
venus
uranus
saturn
-------- +
neptune
Each of the ten letters (m, a, r, s,
v, e, n, u, t, and p) represents a
digit in the range 0 up to 9 (equal letters represent equal
digits and different letters represent different digits).
Furthermore, the digits 1 and 6 are being used most frequently.
| |
|
The Question:
What number does neptune represent?
| |
|
The Answer:
Click here!...
| |
|
back to index
| |
|
Nineteen Numbers Net
| | 
| |
|
This is the toughest number net on our site! It has nineteen
circles that have to be filled with the numbers 1 up to (and including) 19. These
numbers have to be placed in such a way that all numbers on any horizontal row
and any diagonal line add up to the same sum.
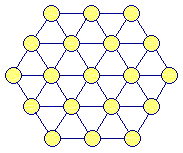
Warning: there are many horizontal and diagonal lines, which have a different number
of circles (3, 4, or 5), nevertheless all these sums have to be equal!
| |
|
The Question:
How should the nineteen numbers be placed in the net?
| |
|
The Answer:
Click here!...
| |
|
back to index
| |
|
Cash for a Car
| |
|
Thanks to Lucas Jones we can present you the following puzzle:
A man is going to an Antique Car auction. All purchases
must be paid for in cash. He goes to the bank and draws out $25,000.
Since the man does not want to be seen carrying that much
money, he places it in 15 envelopes numbered 1 through 15. Each envelope contains
the least number of bills possible of any available US currency (for example, no
two tens instead of a twenty).
At the auction he makes a successful bid of $8322 for a car.
He hands the auctioneer envelopes 2, 8, and 14. After opening the
envelopes the auctioneer finds exactly the right amount.
| |
|
The Question:
How many ones did the auctioneer
find in the envelopes?
| |
|
The Answer:
Click here!...
| |
|
back to index
| |
|
Ladder Alley
| | 
| |
|
In an alley two ladders are placed cross-wise.
The lengths of these ladders are resp. 2 and 3 meters. They cross
one another at one meter above the ground.
| |
|
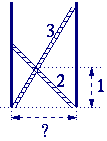
The Question:
What is the width of the alley?
| |
|
The Answer:
Click here!...
| |
|
back to index
| |
|
Cat & Mouse
| | 
| |
|
Four white pieces (the mice) are placed on one side of a chess-board,
and one black piece (the cat) is placed at the opposite side. The game is
played by the following rules:
- Black wins if it reaches the opposite side.
- White wins if it blocks black in such a way that black can not make any move anymore.
- Only diagonal moves (of length 1) on empty squares are allowed.
- White only moves forward.
- Black can move backward and forward.
- Black may make the first move, then white makes a move, and so on...
| |
|
The Question:
Is this game computable (i.e. is
it possible to decide beforehand who wins the game, no matter how hard his
opponent tries to avoid this)?
| |
|
The Answer:
Click here!...
| |
|
back to index
| |
|
Car Parking
| | 
| |
|
A street of length L is randomly
filled with cars (one by one), where the length of a car is the unity of
L (i.e. 1).
| |
|
The Question:
What is the expectation for
the number of cars that can be parked until the street is filled?
| |
|
The Answer:
Click here!...
| |
|
back to index
| |
| |
|
|
Copyright © 1996-2010. RJE-productions. All rights reserved. No part of this website may be published, in any form or by any means, without the prior permission of the authors.
|
