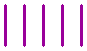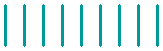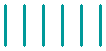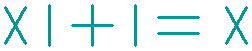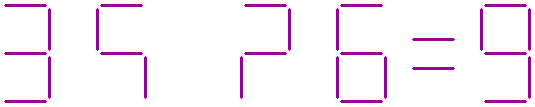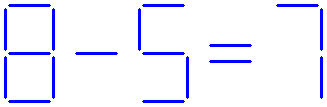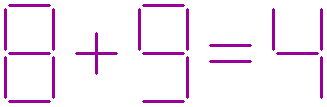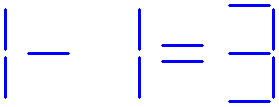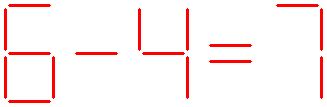Sticking Away Squares ★
Here you see five equal squares.

The question:
Can you leave just three squares by taking away three sticks?

Another question:
Here you see six equal squares.
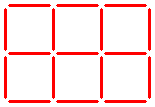
Can you leave just three squares by taking away five sticks?

Yet another question:
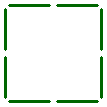
Can you leave two complete squares only, by taking away two sticks from the pattern shown below?


The fourth question:
Can you leave two complete squares only, by taking away eight sticks from the pattern shown below?


The fifth question:
Can you leave six squares only, by taking away eight sticks from the pattern shown below?


The sixth question:
Can you leave three squares only, by taking away six sticks from the pattern shown below?
Triangle Tricks ★
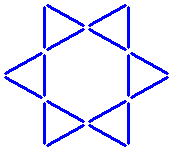
Sixteen sticks form eight equal triangles.
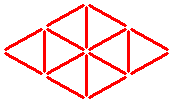

The question:
Can you take away four sticks and leave only four of these triangles?

Another question:
Thirteen sticks form eight triangles (six small ones and two large ones).

Can you take away three sticks and leave only three triangles?

Yet another question:
The nine sticks shown below form three equal triangles.

How can two sticks be moved to make four equal triangles?

The fourth question:
The eighteen sticks shown below form thirteen triangles (nine small ones, three medium ones, and a large one).
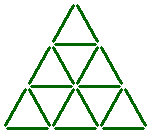
Can you leave only seven of these thirteen triangles by taking away just three sticks?

The fifth question:
The eighteen sticks shown below form thirteen triangles (nine small ones, three medium ones, and a large one).
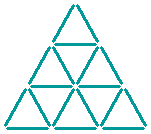
Can you leave only three triangles, of varied sizes, by taking away six sticks?

The sixth question:
These thirteen sticks form six equal triangles.
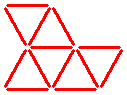
Can you leave only three of these six triangles by removing four sticks?
Jump & Pile ★★
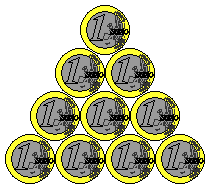
Below you see ten coins in a row.
The goal is to make five piles of two coins.
You must, however, jump over two other coins (these can be two coins next to each other,
but also two piled coins!) to place a coin on top of another coin.
You may jump only with coins that have not been piled yet.

The question:
How can this be done?

A hint :
By clicking on the small arrows, you can move the coins in the desired direction.
Storm-Damage ★★
Peasant Janet kept six pigs in six pens of equal size,
made with thirteen wooden fences (see the picture below).

One night, there was a terrible storm, in which one of the thirteen fences was badly damaged.
Janet rearranged the remaining fences so that the six pigs still each had pens of equal size.

The question:
How did she do that?
Penny through the Paper ★★
Take a coin from your wallet (a 1 or 2 Euro piece works best).
Take a piece of paper and cut a circular hole in it middle, which is slightly smaller than the size of the coin
(a diameter which is roughly 80% of the diameter of the coin, see picture).
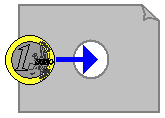

The question:
How can you get the coin through the hole without breaking or cutting the paper?
Six-Sided Stick Shape ★★
The twelve sticks shown below form a six-sided shape containing six triangles.


The question:
Can you make three triangles by moving four sticks?

Another question:
Starting with the same six-sided shape, can you make four equal rhombs by moving exactly three sticks?

Yet another question:
Starting with the same six-sided shape, can you make four equal rhombs by moving exactly four sticks?
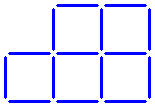
Squared Sticks ★★
Twelve sticks form four equal squares.


The question:
How can exactly four sticks be moved to make three equal squares?

Another question:
Twelve sticks form four equal squares.

How can exactly three sticks be moved to make three equal squares?

Yet another question:
Sixteen sticks form five squares.
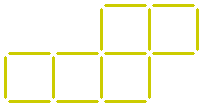
Can you make four squares from this by moving two sticks?

The fourth question:
Sixteen sticks form five squares.
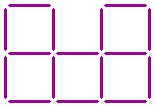
Can you turn these five squares into four squares by moving three sticks?

The fifth question:
Twenty sticks form seven equal squares.
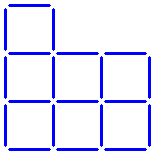
How can three sticks be moved to make five equal squares?

The sixth question:
By moving only two sticks, these three equal sized squares can be changed into four equal sized rectangles.

How can this be done?

The seventh question:
Here you see two squares.
Can you form three squares by moving four sticks?


The eighth question:
The figure below contains five squares (four small ones and a large one).
Can you form seven squares by moving just two sticks, without having overlapping sticks?


The ninth question:
The figure below contains five squares (four small ones and a large one).
Can you form ten squares by moving just four sticks?

Stick Shapes ★★
There are four squares in the pattern shown below.
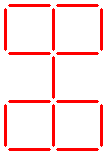

The question:
How can two sticks be moved to make five equal squares?

Another question:
Below you see a hexagon formed by six sticks.
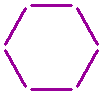
Can you turn this hexagon into two rhombs by moving two sticks and adding one?

Yet another question:
Can you make four equal triangles from the pattern shown below, by moving exactly four sticks?


The fourth question:
Twelve sticks form one square and four triangles.
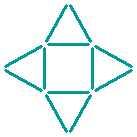
Can you move six sticks to make three squares and one triangle?

The fifth question:
Can you make two squares from the pattern shown below, by moving four sticks?
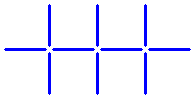

The sixth question:
Can you make three equal squares from the pattern shown below, by moving just three sticks?
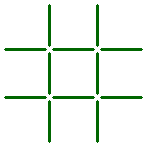

The seventh question:
Can you form three touching triangles from the pattern shown below, by moving exactly three sticks?
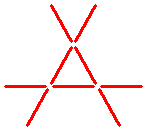

The eighth question:
Can you form three triangles from the pattern shown below, by moving three sticks?
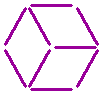
Sunny Summer ★★★
The square cards below must be arranged into one large square.
Two cards may, however, only be laid against each other if the (half) suns are of the same color.
|
|
|
|

The question:
How can this be done?

A hint :
You can drag the cards over the field using your mouse.
It is also possible to move all cards together by "dragging" the field.
Mathematical Sticks ★★★

The question:
Can you balance the equation shown below, by moving exactly three sticks?


Another question:
The equation shown below is not correct.
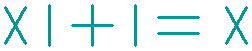
How can you make this equation correct, without moving a single stick?

Yet another question:
In the equation shown below, three sticks are missing.
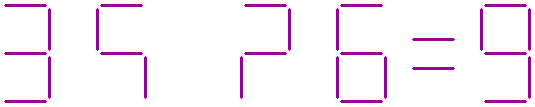
Where should the three missing sticks be placed to make the equation correct?

The fourth question:
In the equation shown below, four sticks are missing.
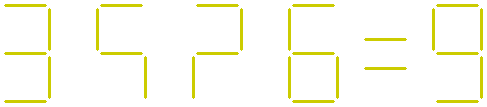
Where should the four missing sticks be placed to make the equation correct?

The fifth question:
The equation shown below is not correct.
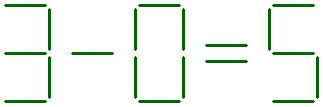
Can you balance this equation, by adding two sticks?

The sixth question:
The equation shown below is not correct.
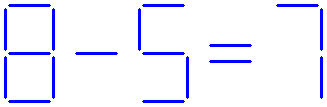
Can you balance this equation, by removing two sticks?

The seventh question:
The equation shown below is not correct.
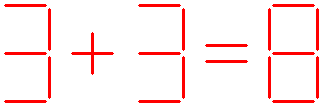
Can you balance this equation, by moving just one stick?

The eighth question:
The equation shown below is not correct.
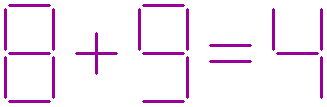
This equation can be balanced by removing three sticks.
There are three ways to do this.
Which are these three ways?

The ninth question:
The equation shown below is not correct.
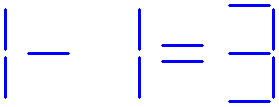
Can you balance this equation, by moving four sticks?

The tenth question:
The equation shown below is not correct.
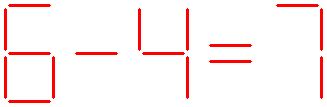
Can you balance this equation, by removing two sticks?

The eleventh question:
The equation shown below is not correct.
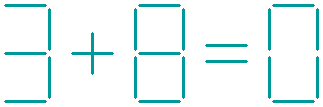
Can you balance this equation, by removing two sticks?
Solitaire ★★★
In this game, there are 32 pieces in a playing field with 33 places.
You can only jump over a piece, if there is a free place directly behind this piece.
You may jump horizontally or vertically.
Every piece that has been jumped over, is removed from the field.
The goal of this game is to leave exactly one piece, in the middle of the playing field.

The question:
How can this be done?

A hint :
By clicking on the small arrows, you can move the pieces in the desired direction.
Stick Tricks ★★★

The question:
How can eleven sticks be rearranged to make nine (without taking any away)?


Another question:
Can you rearrange these three sticks to make nine?


Yet another question:
How can nine sticks be rearranged to make ten?
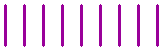

The fourth question:
Can you rearrange these five sticks to make fourteen?
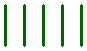
Tricky Sticks ★★★

The question:
Can you rearrange the nine sticks to make a pattern containing three squares?


Another question:
These twelve sticks form five squares (four small ones and a large one).
How can two sticks be moved to make seven squares?
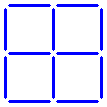

Yet another question:
Can you make four equal triangles, of the same size as the triangles shown below, using just six sticks?


The fourth question:
Can you rearrange these eight sticks to make two squares and four triangles?


The fifth question:
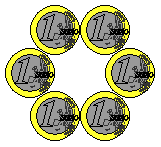
In the pattern shown below, you see six equal squares.
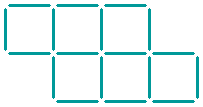
Can you make a pattern containing only three squares by moving four sticks?

The sixth question:
The figure below contains five equal sized squares.
Can you form six equal sized squares by moving just three sticks?